在上一篇文章的最后,我们画出了一张差分分布表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f |
|---|
| 0 | 16 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 1 | - | - | 6 | - | - | - | - | 2 | - | 2 | - | - | 2 | - | 4 | - |
| 2 | - | 6 | 6 | - | - | - | - | - | - | 2 | 2 | - | - | - | - | - |
| 3 | - | - | - | 6 | - | 2 | - | - | 2 | - | - | - | 4 | - | 2 | - |
| 4 | - | - | - | 2 | - | 2 | 4 | - | - | 2 | 2 | 2 | - | - | 2 | - |
| 5 | - | 2 | 2 | - | 4 | - | - | 4 | 2 | - | - | 2 | - | - | - | - |
| 6 | - | - | 2 | - | 4 | - | - | 2 | 2 | - | 2 | 2 | 2 | - | - | - |
| 7 | - | - | - | - | - | 4 | 4 | - | 2 | 2 | 2 | 2 | - | - | - | - |
| 8 | - | - | - | - | - | 2 | - | 2 | 4 | - | - | 4 | - | 2 | - | 2 |
| 9 | - | 2 | - | - | - | 2 | 2 | 2 | - | 4 | 2 | - | - | - | - | 2 |
| a | - | - | - | - | 2 | 2 | - | - | - | 4 | 4 | - | 2 | 2 | - | - |
| b | - | - | - | 2 | 2 | - | 2 | 2 | 2 | - | - | 4 | - | - | 2 | - |
| c | - | 4 | - | 2 | - | 2 | - | - | 2 | - | - | - | - | - | 6 | - |
| d | - | - | - | - | - | - | 2 | 2 | - | - | - | - | 6 | 2 | - | 4 |
| e | - | 2 | - | 4 | 2 | - | - | - | - | - | 2 | - | - | - | - | 6 |
| f | - | - | - | - | 2 | - | 2 | - | - | - | - | - | - | 10 | - | 2 |
为了分析接下来的 CipherThree,我们需要做一个抽象,定义一下 差分特征(differential characteristic):两个具有差分 α 的输入,在经过操作 S[⋅] 后得到两个具有差分 β 的输出,那么这一对 (α,β) 就被称为 差分特征,可以表示为 αSβ.
CipherThree
c=S[S[S[m⊕k0]⊕k1]⊕k2]⊕k3
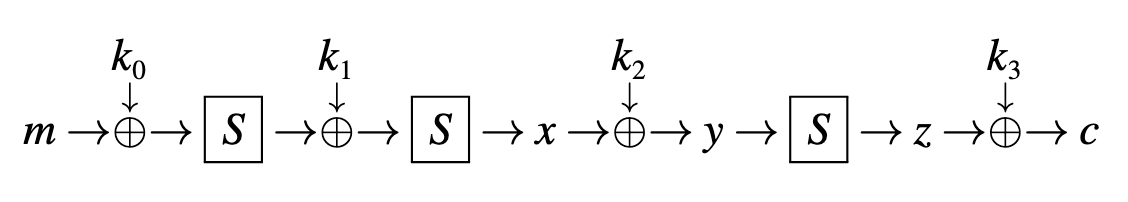 按照前面所说的对 CipherTwo 的攻击,攻击者猜测 k3,计算 y0 和 y1,计算 x0⊕x1. 为了验证猜测是否正确,攻击者输入的消息 需要通过 2 个 S 盒.
按照前面所说的对 CipherTwo 的攻击,攻击者猜测 k3,计算 y0 和 y1,计算 x0⊕x1. 为了验证猜测是否正确,攻击者输入的消息 需要通过 2 个 S 盒.
从差分分布表中,我们可以读出:
- 两个具有差分 f 的消息,以 1610 的概率产生具有差分 d 的输出.
- 两个具有差分 d 的消息,以 166 的概率产生具有差分 c 的输出.
因此我们可以组合两个 S 盒的操作:
- 对第 1 个 S 盒使用特征 fSd.
- 对第 2 个 S 盒使用特征 dSc.
如果假设这些特征是相互独立的,那么这个 2 轮特征 fSdSc 的概率就是 1610×166. 也就是说,攻击者输入具有差分 f 的消息,可以以 6415 的概率预期 y0⊕y1 的值是 c. 给定足够多的明文-密文对,像 CipherTwo 的攻击那样操作,我们就可以恢复密钥 k3.
CipherFour
CipherFour 是一个 r 轮的迭代加密,块大小为 16-bit.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
| P [i] | 0 | 4 | 8 | 12 | 1 | 5 | 9 | 13 |
| i | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| P [i] | 2 | 6 | 10 | 14 | 3 | 7 | 11 | 15 |
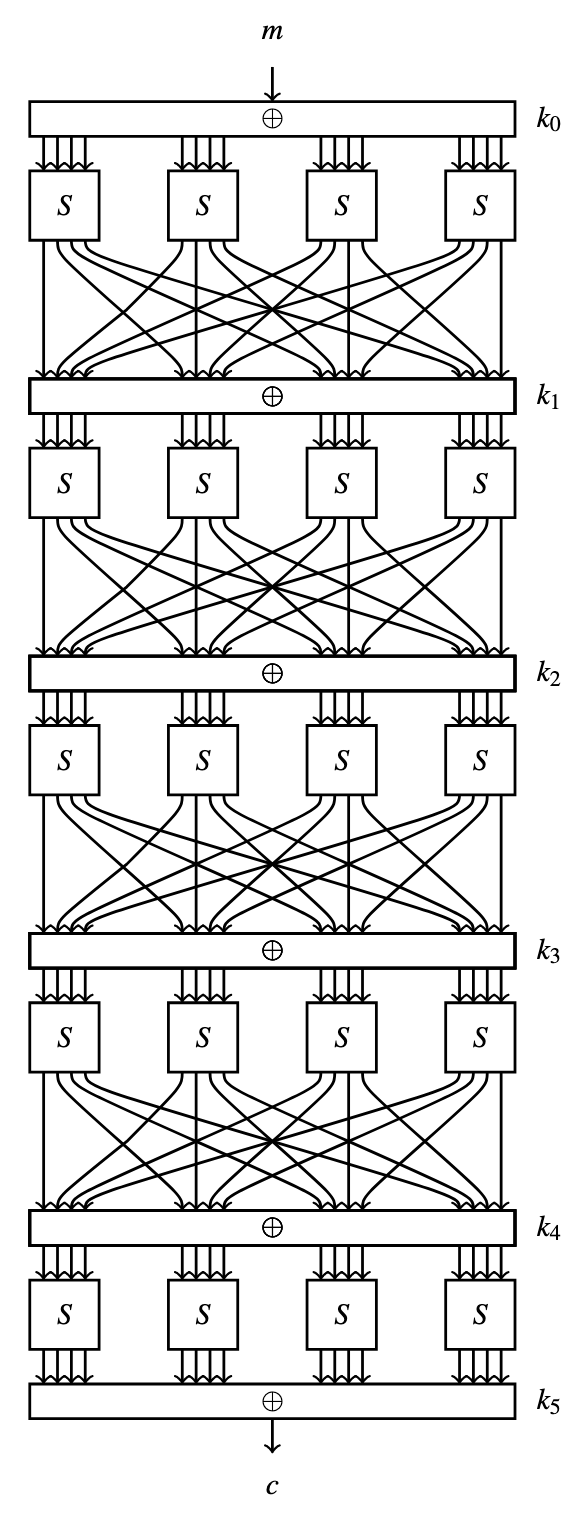 让我们考虑对 CipherFour 的差分攻击. 如果我们试图进行 CipherThree 中类似的攻击,那么首先需要找到一个特征,这个特征可以预测 r−1 轮后两个部分加密的消息的差分. 如果能够找到一个具有足够高概率的特征,那么原则上,我们就能够恢复轮密钥 kr.
让我们考虑对 CipherFour 的差分攻击. 如果我们试图进行 CipherThree 中类似的攻击,那么首先需要找到一个特征,这个特征可以预测 r−1 轮后两个部分加密的消息的差分. 如果能够找到一个具有足够高概率的特征,那么原则上,我们就能够恢复轮密钥 kr.
为了构建多轮的特征,我们先尝试找到 一轮的特征.
一轮的特征
我们需要研究 4 个 S 盒,找到存在高概率输出差分的输入差分. 由于 P 盒是线性的,可以直接计算一轮的输入差分. 4 个 S 盒的输入和输出差分可以记为
(α1,α2,α3,α4)S(β1,β2,β3,β4)
其中 αi 是输入到每个 S 盒的值 Ai 之间的差分,βi 是输出值 S[Ai] 之间的差分.
因为 P 盒是固定的,我们可以 确切地预测 差分通过 P 盒发生的变化
(β1,β2,β3,β4)P(γ1,γ2,γ3,γ4)
其中 β1∥β2∥β3∥β4 是 P 盒 16-bit 的输入差分. 对于一整轮 R,
(α1,α2,α3,α4)R(γ1,γ2,γ3,γ4)
表示 CipherFour 一轮的特征.
注意到差分分布表左上角的项是 16,也就是说「输入差分为 0 时,输出差分为 0」发生的概率为 1. 很显然,对于相同的输入,S 盒会有相同的输出,选择所有 4 个 S 盒输入差分都为 0 会得到一个概率为 1 的一轮特征. 但这对密码分析来说没有意义,一个 非平凡 的一轮特征必须最多具有 3 个输入差分为 0 的 S 盒.
我们考虑发生概率为 1610 的特征
(0,0,0, f)S(0,0,0, d)
经过 P 盒
(0,0,0, d)P(1,1,0,1)
这就得到了完整的一轮
(0,0,0, f)R(1,1,0,1)
在这个基础上再扩展一轮,发生概率为 (166)3 的特征
(1,1,0,1)S(2,2,0,1)
经过 P 盒
(2,2,0,2)P(0,0, d,0)
假设两个一轮特征相互独立,那么我们就得到了 CipherFour 的一个发生的概率为 1610×(166)3=4096135 的二轮特征
(0,0,0, f)R(1,1,0,1)R(0,0, d,0)
注意,上面描述的过程从差分分布表中查找每个 S 盒最高概率的特征. 但是这样找到的特征可能在一轮中是最佳的,但其他密码组件(例子中为 P 盒)可能会让这个特征在多轮中变得不那么理想.
例如,我们考虑输入差分 (0,0,2,0),发生概率为 166 的一轮差分
(0,0,2,0)R(0,0,2,0)
由于输入差分等于输出差异,这个特征可以与其自身连接,产生我们想要的任意多轮的特征. 这样的特性称为 迭代特性. 我们有概率为 (166)2 的二轮差分
(0,0,2,0)R(0,0,2,0)R(0,0,2,0)
概率为 (166)3 的三轮差分
(0,0,2,0)R(0,0,2,0)R(0,0,2,0)R(0,0,2,0)
概率为 (166)4 的四轮差分
(0,0,2,0)R(0,0,2,0)R(0,0,2,0)R(0,0,2,0)R(0,0,2,0)
类似前几次攻击,如果攻击者选择输入差分 (0,0,2,0) ,从密文反向计算,根据四轮后部分加密的密文中的差异是否符合预期,得到最后一个子密钥 k5(的某些位).
这样做的问题是:这个差分发生的概率是 0.02,而随机指定的差分发生的概率是 161>0.02 ,无法从中有效区分出正确的密钥信息. 在下一篇文章中我们会解决这个问题.
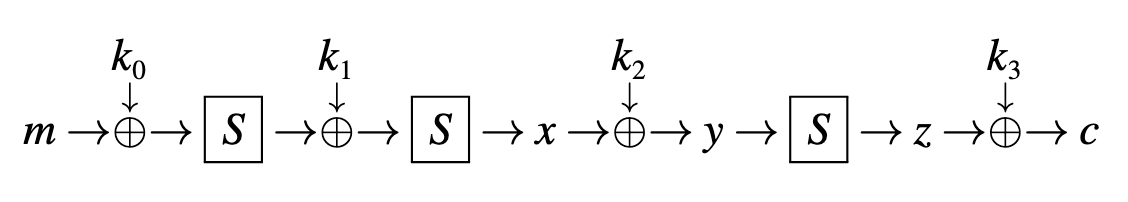 按照前面所说的对 CipherTwo 的攻击,攻击者猜测 ,计算 和 ,计算 . 为了验证猜测是否正确,攻击者输入的消息 需要通过 2 个 S 盒.
按照前面所说的对 CipherTwo 的攻击,攻击者猜测 ,计算 和 ,计算 . 为了验证猜测是否正确,攻击者输入的消息 需要通过 2 个 S 盒. 让我们考虑对 CipherFour 的差分攻击. 如果我们试图进行 CipherThree 中类似的攻击,那么首先需要找到一个特征,这个特征可以预测 轮后两个部分加密的消息的差分. 如果能够找到一个具有足够高概率的特征,那么原则上,我们就能够恢复轮密钥 .
让我们考虑对 CipherFour 的差分攻击. 如果我们试图进行 CipherThree 中类似的攻击,那么首先需要找到一个特征,这个特征可以预测 轮后两个部分加密的消息的差分. 如果能够找到一个具有足够高概率的特征,那么原则上,我们就能够恢复轮密钥 .